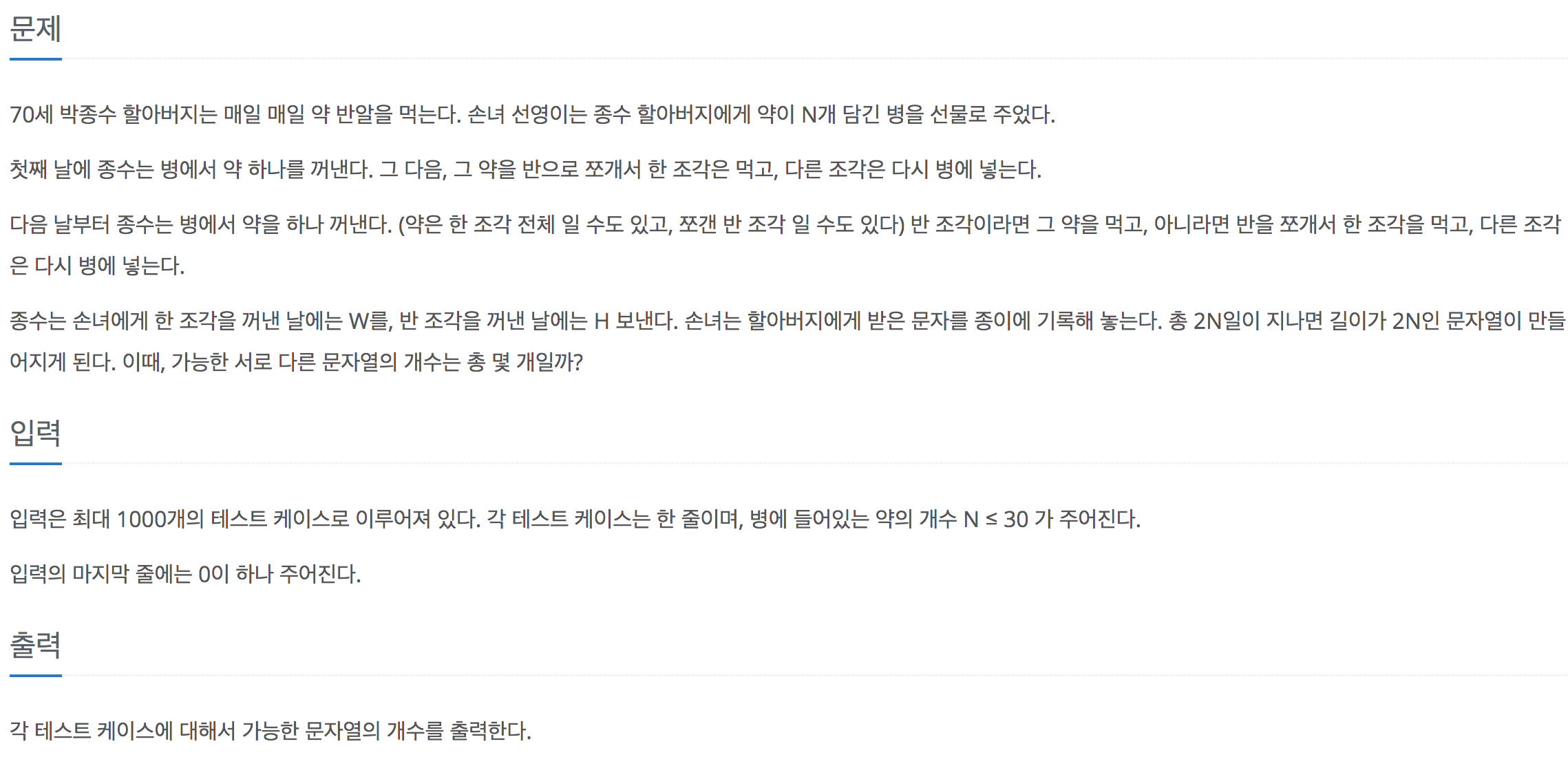

이 문제는 동적계획법(DP)으로 풀 수 있는 문제이다. 그 이유는 완전한 알약 갯수와 반쪽 짜리 알약 갯수가 주어질 때, 문자열의 경우의 수는 일정하기 때문이다. 따라서 DP는 다음과 같이 정의 할 수 있다.
dp[w][h] = 완전한 알약이 w 개 있고, 반쪽 짜리 알약이 h 개 있을 때, 문자열의 경우의 수
dp[w][h] = dp[w-1][h+1] + dp[w][h-1]
Top-Down
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
typedef long long ll;
ll dp[33][66];
ll solve(int w, int h){
if(w == 0)
return 1;
ll& ret = dp[w][h];
if(ret != 0)
return ret;
ll s = solve(w-1, h+1);
if(h > 0)
s = s + solve(w, h-1);
return ret = s;
}
|
cs |
Bottom-Up
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
typedef long long ll;
ll dp[33][66];
// 초기화
for(int h=1; h<=60;h++)
dp[0][h] = 1;
dp[1][0] = 1;
for(int w=1; w<=30; w++){
for(int h=0; h<=60; h++){
dp[w][h] = dp[w-1][h+1] + (h > 0 ? dp[w][h-1] : 0);
}
}
|
cs |
이 문제는 초기화만 잘 해준다면 Top-Down 방식과 코드가 큰 차이가 없이 Bottom-Up 또한 꽤 직관적인 코드가 짜여진다.
전체 소스 코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
#include<stdio.h>
int n;
typedef long long ll;
ll dp[33][66];
ll inline max(ll a, ll b){return a>b?a:b;}
ll solve(int w, int h){
if(w == 0)
return 1;
ll& ret = dp[w][h];
if(ret != 0)
return ret;
ll s = solve(w-1, h+1);
if(h > 0)
s = s + solve(w, h-1);
return ret = s;
}
int main(){
// solve(30, 0);
for(int h=1; h<=60;h++)
dp[0][h] = 1;
dp[1][0] = 1;
for(int w=1; w<=30; w++){
for(int h=0; h<=60; h++){
dp[w][h] = dp[w-1][h+1] + (h > 0 ? dp[w][h-1] : 0);
}
}
while(1){
scanf("%d",&n);
if(n==0) break;
printf("%lld\n", dp[n][0]);
}
return 0;
}
|
cs |
'알고리즘 문제풀이' 카테고리의 다른 글
| LCS 최장 공통 부분 수열 (0) | 2020.09.03 |
|---|---|
| BOJ 가장 긴 증가하는 부분 수열 (0) | 2020.09.02 |
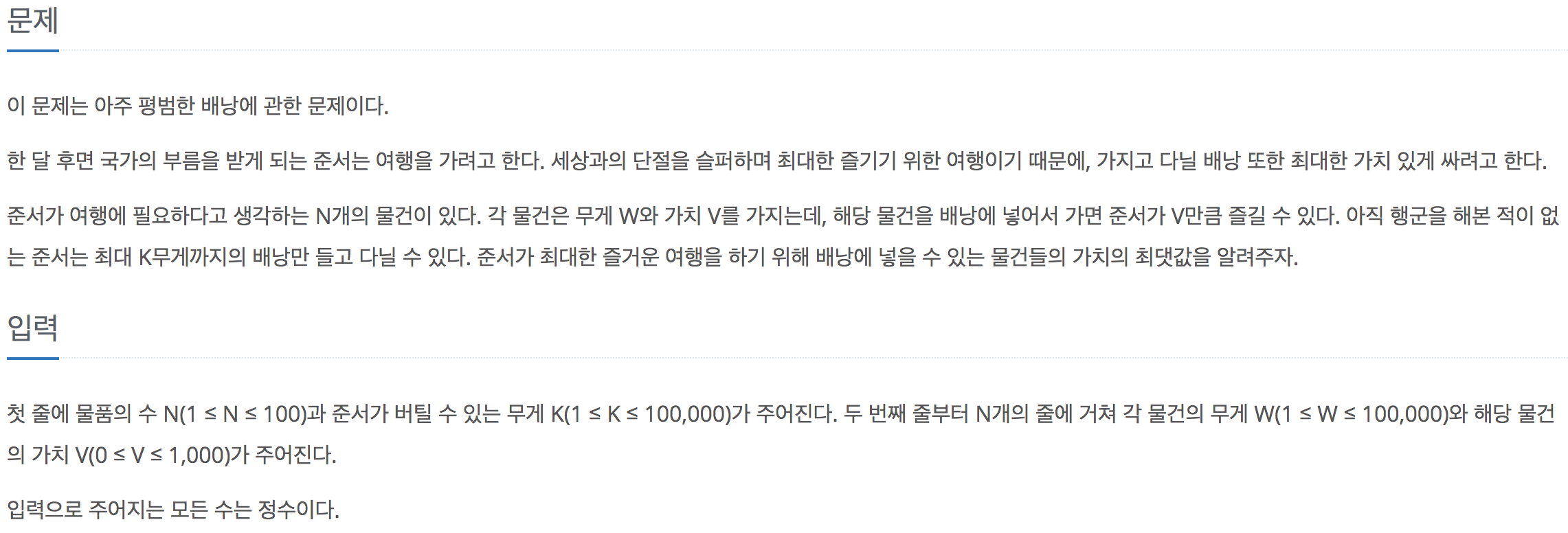
| BOJ 12865 평범한 배낭 (0) | 2020.08.28 |
| BOJ 15649~15650 N과 M (0) | 2020.08.20 |
| BOJ 2580 스도쿠 (0) | 2020.08.20 |