uang's blog

공통 정보 정의하고 재사용하는 방법

www.acmicpc.net/problem/17472

이 문제는 DFS, MST(최소신장트리) 를 이용해 푸는 문제이다. 질문 게시판을 보니 삼성 코딩테스트 기출문제인듯 하다. 위 문제 풀이 방법 중 핵심은 인접한 셀들을 "섬"으로써 잘 Grouping 하여, 다른 "섬"(group)과의 최단거리를 찾아야 한다. 

일단 필요한 알고리즘들을 생각해보면,

   1. DFS : 섬의 개수 세기

   2. MST(최소신장트리) : 모든 섬들을 연결하는 최단 간선 구하기 

이다.

MST 에는 크루스칼(Kruskal) 알고리즘, 프림(prim) 알고리즘이 있다. 

크루스칼 알고리즘

간선의 가중치를 정렬해 작은 것 부터 차례로 선택해나가는 방법

1. 간선들을 가중치의 오름차순으로 정렬한다
2. 정렬된 간선 중 사이클을 형성하지 않는 간선을 선택
3. 해당 간선을 현재 MST 집합에 추가
4. 1~3 과정을 "|정점 수| - 1" 번 반복  // V 개의 정점을 연결하기 위해 필요한 간선은 V-1개 이므로

프림 알고리즘

하나의 정점을 선택해 가장 가중치가 작은 간선들을 차례로 연결해나가는 방법

1.  시작 노드(어떤 노드든 상관없음) 를 MST 집합에 포함
2.  1단계에서 만들어진 MST 집합에 인접한 노드들 중 최소 간선으로 연결된 노드를 선택해 MST 집합에 포함
3.  1~2 과정을 "|정점 수| - 1" 번 반복  // V 개의 정점을 연결하기 위해 필요한 간선은 V-1개 이므

프림알고리즘의 구현을 위해선 priority_queue(우선순위 큐)가 필요할 수 있지만, 본 문제에서는 간선을 우리가 만들어가며 찾아야하기 때문에 BFS(너비우선탐색)를 통해 찾는 것이 적절하다. 같은 이유로 Kruskal 알고리즘을 사용하기 복잡하다.

대략 알고리즘을 설명하면 다음과 같다.

1. 섬의 갯수 찾기 (DFS)

    - 각 섬의 Grouping을 위해 ID 를 부여한다.

2. 섬의 갯수-1 번 반복하여 다른 그룹의 섬을 잇는 간선 찾기 (BFS)

    - 1번 섬을 기준으로 BFS를 통해 최단거리의 다른 섬(그룹)을 찾으면 1번 그룹에 병합 (Union-Find 개념)

    * 탐색 할 때는 가로/세로 방향 유지

* Union-Find 알고리즘 참고 : https://gmlwjd9405.github.io/2018/08/31/algorithm-union-find.html

소스코드

#include<stdio.h>
#include<vector>
#include<queue>
#include<string.h>
using namespace std;
 
struct node{
    pair<int,int> cur;
    int cnt_bridge, is_vertical;
    node(pair<int,int> cur, int  cnt, int is_v) : cur(cur), cnt_bridge(cnt), is_vertical(is_v)  {};
};
 
int n,m, dx[4]= { -1,1,0,0}, dy[4] = {0,0,-1,1}, arr[11][11];
bool visited[11][11][2];
vector< pair<int,int> > island[7];
 
void find_island(int idx, int y,int x){
    visited[y][x][0] = 1;
    island[idx].push_back(make_pair(y,x));
    arr[y][x] = idx+1;
    for(int i=0;i<4;i++){
        int ny = y + dy[i], nx = x+dx[i];
        if(ny>=0 && nx >=0 && nx < m && ny < n){
            if(!visited[ny][nx][0] && arr[ny][nx]){
                find_island(idx, ny, nx);
            }
        }
    }
}
 
void push_queue(queue< node >& q, int island_idx=1){
    int idx = island_idx-1; // 1번 그룹 
 
    for(int i=0; i< island[idx].size(); i++){
        q.push(node(island[idx][i], 0, -1));
    }
    // printf("push queue #%d, queue_size : %d\n", island_idx, q.size());
}
 
void Union(int found_island_idx){
    int& idx = found_island_idx;
    for(int i=0;i<n; i++){
        for(int j=0; j<m;j++){
            if(arr[i][j] == idx){
                island[0].push_back(make_pair(i,j));
                arr[i][j] = 1;
            }
        }
    }
 
    // printf("union between 1 and %d\n\n", idx);
    // for(int i=0;i<n; i++){
    //     for(int j=0; j<m;j++){
    //         printf("%d ",arr[i][j]);
    //     }
    //     printf("\n");
    // }
}
 
int main(){
    scanf("%d%d",&n,&m);
    for(int i=0;i<n;i++){
        for(int j=0; j<m; j++){
            scanf("%d", &arr[i][j]);
        }
    }
    int cnt_island = 0;
    for(int i=0; i<n;i++){
        for(int j=0; j<m;j++){
            if(!visited[i][j][0] && arr[i][j]){
                find_island(cnt_island, i,j);
                cnt_island += 1;
            }
        }
    }
 
    // printf("\n");
    // for(int i=0; i<n;i++){
    //     for(int j=0; j<m;j++){
    //         printf("%d ", arr[i][j]);
    //     }
    //     printf("\n");
    // }
    // cnt_islend-1 edges are needed to connect all island
    int ans = 0, edges = 0;
    for(int i=0; i<cnt_island-1; i++){
        memset(visited, 0, sizeof(visited));
        queue< node > q;
        push_queue(q, 1); 
 
        while(!q.empty()){
            node cur = q.front(); q.pop();
            int cury = cur.cur.first, curx = cur.cur.second;
 
            // another island check
            if(arr[cury][curx] > 1 && cur.cnt_bridge >= 2) {
                // printf("found another island#%d at (%d,%d): %d\n", arr[cury][curx], cury,curx, cur.cnt_bridge);
                int island_idx = arr[cury][curx];
                ans += cur.cnt_bridge;
                edges += 1;
                Union(island_idx);
                break;
            }
 
            // cannot pass through another island
            if(arr[cury][curx] > 1){
                continue;
            }
 
            if(cur.is_vertical == -1){
                visited[ cury ][ curx ][0] = visited[ cury ][ curx ][1] = 1;
            } else {
                visited[ cury ][ curx ][cur.is_vertical] = 1;
            }
 
            // build  bridge to search island
            for(int d=0; d<4;d++){
                int ny = cury + dy[d], nx = curx + dx[d];
                if(ny >= 0 && nx >=0 && nx < m && ny < n && arr[ny][nx] != 1 && !visited[ny][nx][cury!=ny]){
                    if( cur.is_vertical == -1 ){ // all directions
                        q.push(node(make_pair(ny,nx), cur.cnt_bridge+(arr[cury][curx] == 0?1:0), cury != ny));
                    } else if (cur.is_vertical == 1 && cury != ny){
                        q.push(node(make_pair(ny,nx), cur.cnt_bridge+(arr[cury][curx] == 0?1:0), 1));
                    } else if (cur.is_vertical == 0 && cury == ny) { // horizontal
                        q.push(node(make_pair(ny,nx), cur.cnt_bridge+(arr[cury][curx] == 0?1:0), 0));
                    }
                }
            }
        }
    }
    printf("%d\n", (ans == 0 || edges != cnt_island-1) ? -1 : ans);
    return 0;
}
 

www.acmicpc.net/problem/1305

위 문제는 길이가 N 인 광고판에 문자열 길이가 L 인 광고가 왼쪽 쉬프트를 하며 무한히 나타날 때, 가능한 문자열의 최소 길이를 구하는 문제이다. 즉, 광고판 길이가 6이고 현재 광고판의 문자열이 "aabaaa" 일때, 가능한 문자열 후보는 "aaba", "aaab", "abaa", "aabaa", "abaaa" 등 다양하지만, 가장 짧은 길이는 4이다.

이 문제는 KMP 알고리즘에서 사용하는 pi 배열을 이용하여 풀 수 있다. pi 배열은 접두사(prefix) 와 접미사(suffix)가 같은 부분 문자열 중 가장 길이가 긴 것을 저장한다.

"ABADABC" 라는 문자열이 있을 때, pi는 다음과 같이 저장된다.

KMP는 이 pi배열을 이용해 문자열 검색의 시간 복잡도를 O( |S| * |P| ), (S : 전체 문자열, P : 전체 문자열에서 찾고자하는 패턴(검색) 문자열) 에서 O( |S|+|P| ) 로 줄이는 알고리즘이다.

1305 광고문제는 검색까지는 필요없고, Pi만 배열만 있으면 풀 수 있다.

길이가 N인 광고판과 길이가 L (L <= N) 인 문자열이 있을 때, 앞의 X개의 문자열(진한 파란색)은 광고 문자열 L번째 문자 뒤에 반복된다.

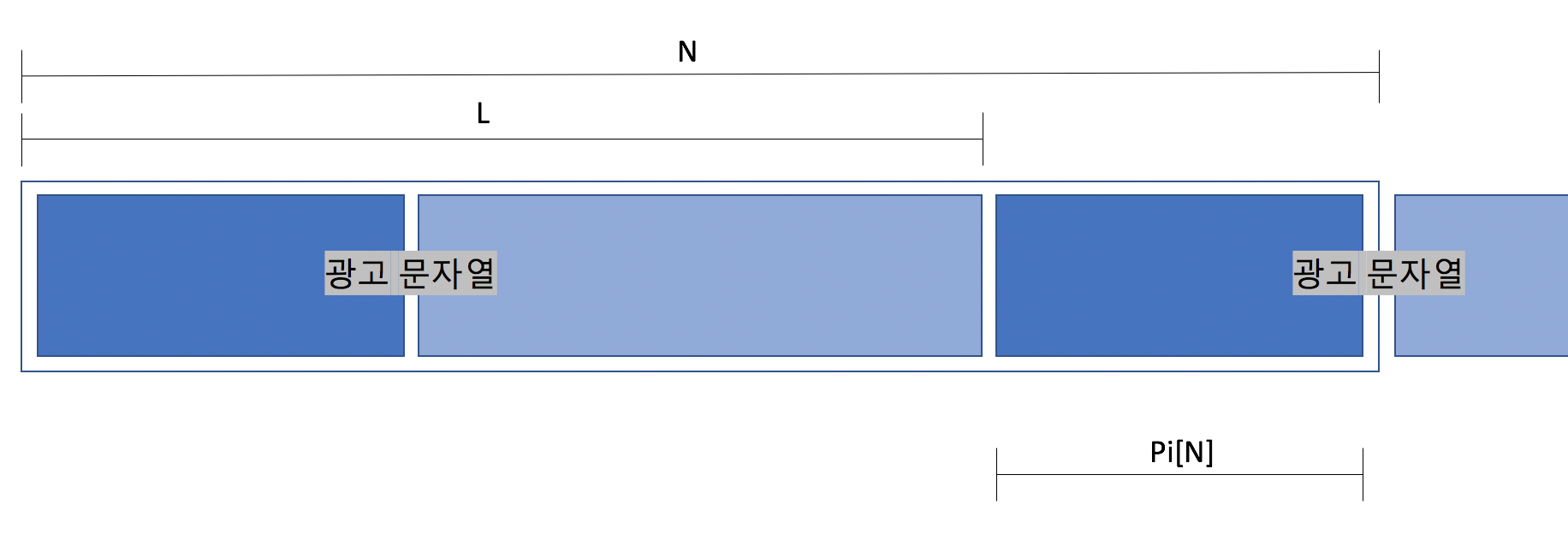
즉, N길이의 광고판 문자열에 대해 pi 를 구한 후, N-pi[N]을 구하면 답을 구할 수 있다.

소스코드

소스는 백준님 풀이 방식을 기반으로 구현했습니다.

#include<iostream>
#include<string>
#include<vector>
using namespace std;
 
vector<int> get_pi_array(string s){
    int n = s.size();
    vector<int>pi(n);
    pi[0] = 0;
    int j = 0;
    for(int i=1; i < n; i++){
        while(j>0 && s[i] != s[j]){
            j = pi[j-1];
        }
        if(s[i] == s[j]){
            pi[i] = j + 1;
            j += 1;
        } else {
            pi[i] = 0;
        }
    }
    return pi;
}
 
int main(){
    int n;
    string s;
    cin >> n >> s;
    vector<int> pi = get_pi_array(s);
    cout << n - pi[n-1] << '\n';
    return 0;
}

관련 사이트:

bowbowbow.tistory.com/6

m.blog.naver.com/kks227/220917078260